飼料配方是畜牧業生產中的重要環節,配方的好壞決定畜牧產品的質量和經營者的生產效益,因此,配方的原則通常是在滿足飼養標準的情況下盡量降低配方的成本,也就是說追求一個最低成本.這是一個非常復雜難解的問題,一般采用以下兩種方法進行求解:線性規劃和目標規劃,其中,線性規劃是Waugh在1951年提出將其應用于該領域,并且用得最為普遍,其主導思想是將配方問題用線性規劃問題建模,并用單純型法進行求解,由于線性規劃的剛性太強,導致利用該方法進行配方求解時出現無最優解的情況十分頻繁,給出的參考解也不適用,因此,這種方法在實際生產中發揮的指導作用并不大.將目標規劃方法應用于該領域,就是為了克服線性規劃求不出最優解的弱點,目標規劃的思想是事先設定一個可接受的成本值,然后在優先滿足某些(部分)約束而忽略其他約束的情況下獲得接近該成本值的一個配方,這種方法相對于線性規劃而言更靈活,但獲得的解不是總有用,有些解可用,有些解不可用,因為,一個問題沒有最優解是由于約束條件中存在無法滿足或相互沖突的約束。目標規劃的方法是為每個約束賦予一個優先級,優先級高的約束先滿足,當用戶為無法滿足或相互沖突的約束賦上高優先級時,會導致系統的解不可用,相反可用,綜上,線性規劃和目標規劃都是采用數學方法對配方問題進行求解,其結果總存在不盡人意的地方,比如,線性規劃多數情況下求不到最優解,目標規劃解的獲得是以人為犧牲某些約束為代價,因此,我們有必要針對飼料配方問題探索一個更具有實際指導意義的問題求解方法.在相關資料中,Bruin等人提出了用多Agent系統求解一種特殊線性規劃問題的理論模型,該模型類似于資源分配,即櫛個Agent共享m個資源,每個Agent有自己的任務(相當于約束滿足問題),假設在Agent具有任意r個資源時,該agent所對應的問題有解,該模型解決了咒個Agent通過協商方式協調資源比例的問題,采用的方法是在保持資源總數不變的前提下,AgentA減少一定的比例占,agent B相應增加一定的比例占,兩個Agent呵以協商艿的取值。本文就是在借鑒了文獻[2]的思想后,做了大量實驗研究的基礎上提出了一個基于多Agent系統的配方問題求解模型。
三門峽富通新能源生產的飼料
顆粒機、顆粒機、飼料機組是養殖戶們不錯的選擇。
1、飼料配方問題簡介
飼料配方問題簡言之就是將凡種飼料原料以一定比例混合在一起得到一種混合后的飼料,要求該飼料中的某些營養成分達到(某種動物的)飼養標準。
表4例1最優解約束滿足情況表
例1.如選擇表1所示“生長豬0~120kg采食3075g NRC_98”的飼養標準,原料選擇情況如表2所示,得到圖1所示的數學模型.即在滿足約束條件(1)~(11)的前提下,求目標函數z的最小值(最。低成本).利用線性規劃方法對該問題求解,可得到如表3所示的最優解,約束滿足情況如表4所示:

表1 飼料標準中要求的各營養元素含量
|
參算指標 |
標準值(%) |
|
消化能 |
3.40 |
|
粗蛋白 |
13.20 |
|
鈣 |
0.45 |
|
磷 |
0.40 |
|
賴氨酸 |
0.60 |
|
蛋氨酸 |
0.23 |
表2幾種原料及營養成分含量(單位:元、兆卡/千克,%)
|
變量 |
原料名 |
價格(元) |
用量下限 |
用量上限 |
消化能 |
粗蛋白 |
鈣 |
磷 |
賴氨酸 |
蛋氨酸 |
|
X1 |
玉米 |
0.9 |
45 |
99.9 |
3.41 |
8.7 |
0.02 |
0.27 |
0.24 |
0.18 |
|
X2 |
小麥麩 |
1.27 |
0 |
99.9 |
2.24 |
15.7 |
0.11 |
0.92 |
0.58 |
0.13 |
|
X3 |
大豆粕 |
2.86 |
0 |
99.9 |
3.25 |
43 |
0.32 |
0.61 |
2.45 |
0.64 |
|
X4 |
棉籽粕 |
1.48 |
3 |
5 |
2.26 |
42.5 |
0.24 |
0.97 |
1.59 |
0.45 |
|
X5 |
大豆油 |
8 |
0 |
99.9 |
7.7 |
|
|
|
|
|
|
X6 |
石粉 |
0.2 |
0 |
99.9 |
|
|
35.85 |
|
|
|
|
X7 |
磷酸氫鈣 |
2 |
0 |
99.9 |
|
|
23.20 |
18 |
|
|
|
X8 |
蛋氨酸 |
36 |
0 |
0.7 |
|
|
|
|
|
98 |
|
X9 |
賴氨酸 |
28 |
0 |
99.9 |
|
|
|
|
78 |
|

下一頁

定原則來得到保證,結論得證。 證畢。
定理1.如果某配方問題存在最優解,則此算法一定能找到該最優解.
證明,由算法知,算法結束于兩種情況,一種是所有Agent都處于satisfied狀態,另一種是不存在具有unsatisfied狀態的Agent。如果,算法結束于第1種情況,由引理1,算法得到的解是最優解,如果算法結束于第2種情況,則算法得到的一定不是最優解,現在證明算法不會結束于第2種情況,假設算法結束于第2種情況,并得到解又= Xl,X2,…,i。,此時算法已嘗試了所有可能的方案,但都失敗,這與問題存在最優解矛盾,結論得證, 證畢.
6實驗結果及分析
6.1有最優解的情況
對于有最優解的問題,以例1為例,實驗結果如圖2、圖3、圖4所示,其中,z軸表示協商輪數,圖2表示協商過程中噸成本的取值變化情況,圖3表示協商過程中各原料配比的取值變化情況,圖4表示約束條件的實際值一標準值隨協商過程的變化情況。
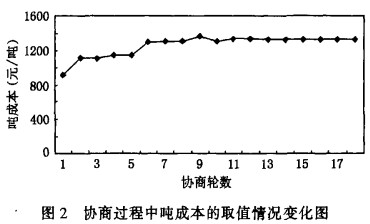
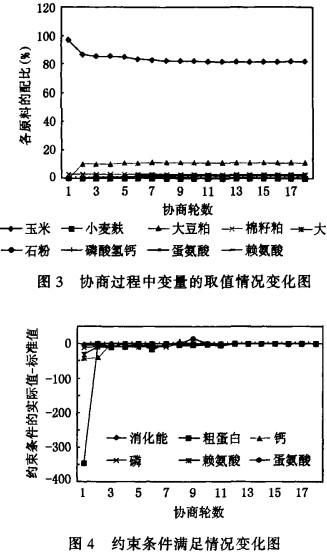
分析:從圖中可以看出,算法最終收斂到一個最優解。
6.2沒有最優解的情況
對于沒有最優解的問題,給定表5所示幾種原料及其營養成分含量,分別用線性規劃、目標規劃和多Agent系統來求解,約束滿足情況如表6所示,其圖解表示如圖5所示,其中,z軸表示的是約束條件,共有8個約束,y軸表示約束條件在算法結束時的取值情況(實際值一目標值)。
表5幾種飼料配方原料及其營養成分含量(單位:元、兆卡/千克、%)
|
變量 |
原料名 |
價格 |
用量下限 |
用量上限 |
消化能 |
粗蛋白 |
鈣 |
磷 |
賴氨酸 |
蛋氨酸 |
蛋+胱 |
色氨酸 |
|
X1 |
玉米 |
0.9 |
45 |
99.9 |
3.41 |
8.7 |
0.02 |
0.27 |
0.24 |
0.18 |
0.38 |
0.07 |
|
X2 |
大豆 |
2.4 |
0 |
10 |
3.97 |
35.50 |
0.27 |
0.48 |
2.00 |
0.48 |
1.03 |
0.56 |
|
X3 |
大豆餅 |
2.19 |
0 |
99.9 |
3.23 |
40.90 |
0.30 |
0.49 |
2.38 |
0.59 |
1.20 |
0.63 |
|
X4 |
石粉 |
0.2 |
0 |
99.9 |
|
|
35.85 |
|
|
|
|
|
|
X5 |
磷酸氫鈣 |
2 |
0 |
99.9 |
|
|
23.20 |
18 |
|
|
|
|
|
X6 |
4%預混料 |
3 |
4 |
4 |
|
|
18.00 |
15.00 |
3.00 |
2.00 |
|
|
表6分別用線性規劃、目標規劃和多Agent系統來求解得到的成本及約束滿足情況表(單位:%,元/噸)
|
問題求解法 |
實際值-標準值(%) |
|
消化能 |
粗蛋白 |
鈣 |
磷 |
賴氨酸 |
蛋氨酸 |
色氨酸 |
蛋+胱 |
成本 |
|
線性規劃(差值) |
0.01 |
6.99 |
-0.15 |
5.79 |
0 |
9.39 |
0.69 |
14.04 |
1149.21 |
|
多Agent(差值) |
0.066 |
0.002 |
0.205 |
0.297 |
-3.977 |
7.297 |
0.038 |
13.963 |
1122.206 |
|
目標規劃(差值) |
-0.213 |
64.194 |
-0.004 |
-9.512 |
0 |
8.155 |
-0.4 |
15.666 |
1134.2 |
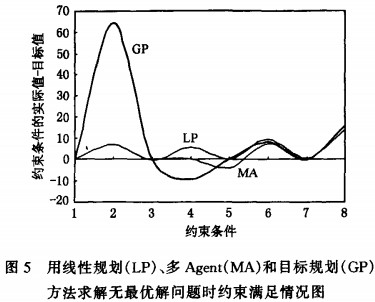
分析:從圖中我們可以看出,用多Agent方法求得的解使問題中各約束滿足得最好(曲線最平滑),因為,飼料配方問題強調營養成分的比例,只有營養成分滿足一定比例時,動物對營養吸收得最好.在這個問題中,線性規劃在發現問題無最優解時結束,結束時各變量的當前值為算法的解;目標規劃首先設定一個噸成本1130.00,然后再將各約束加上優先級,優先級高的約束優先滿足,本例中優先考慮25(賴氨酸)和23(鈣),所求解如表6所示;多Agent方法首先判斷出26(蛋氨酸)和z8(蛋+胱)為不可滿足(unsatisfiable)約束,忽略,繼而判斷出約束z5與Z,Z2,Zl3,Zl4和Zl7相沖突,同樣忽略……最終得到關于Z2和27的最優解,即整個問題的近似解,顯然,這個解優于線性規劃和目標規劃的解.
7結 論
本文提出了一種基于多Agent系統的飼料配方優化算法,對于有最優解的問題,該算法能夠逼近最優解,對于沒有最優解的問題,該算法給出的近似解優于目標規劃方法得到的解。通過實際應用,已經證明,該方法得出的解更具有實際應用價值.另外,該算法還具有一定的可擴展性,即可以擴展到求一般的線性規劃問題。分析:從圖中我們可以看出,用多Agent方法求得的解使問題中各約束滿足得最好(曲線最平滑),因為,飼料配方問題強調營養成分的比例,只有營養成分滿足一定比例時,動物對營養吸收得最好.在這個問題中,線性規劃在發現問題無最優解時結束,結束時各變量的當前值為算法的解;目標規劃首先設定一個噸成本1130.00,然后再將各約束加上優先級,優先級高的約束優先滿足,本例中優先考慮25(賴氨酸)和23(鈣),所求解如表6所示;多Agent方法首先判斷出26(蛋氨酸)和z8(蛋+胱)為不可滿足(unsatisfiable)約束,忽略,繼而判斷出約束z5與21,22,23,24和27相沖突,同樣忽略……最終得到關于zz和27的最優解,即整個問題的近似解,顯然,這個解優于線性規劃和目標規劃的解。
7結 論
本文提出了一種基于多Agent系統的飼料配方優化算法,對于有最優解的問題,該算法能夠逼近最優解,對于沒有最優解的問題,該算法給出的近似解優于目標規劃方法得到的解。通過實際應用,已經證明,該方法得出的解更具有實際應用價值.另外,該算法還具有一定的可擴展性,即可以擴展到求一般的線性規劃問題。
三門峽富通新能源生產的飼料顆粒機、顆粒機、
秸稈壓塊機、
木屑顆粒機是養殖戶和生產成型燃料加工廠不錯的選擇。


 下一頁
下一頁


